Least square residual classifier Part - II

In the Least square residual Part - I, classification algorithm called least square residual classifier based on singular value decomposition was presented and applied on the MNIST handwritten digit recognition task. Please read the mentioned post before proceeding.

In this post, we introduce least square residual classifier based on autoencoders and applied on the same MNIST handwritten digit recognition task.

This Building Autoencoders in Keras post has an excellent explanation on autoencoders.

I am suggesting to read the above mentioned post before proceeding further.

Again as mention in the post, Each digit of specific class \(i=0~\cdots~9\) is assumed to attracted to a certain low dimensional subspace. Such compression of the digit vector of class \(\alpha\) to the corresponding low dimensional subspace is done by the encoding segment of the autoencoder belonging to class \(\alpha\).

After compression, the digit can be reconstructed by the decoding segment of the same autoencoder. The resultant reconstruction error of the unknown digit from all the encoders of 10 digits is used as a yard stick to classify the digit.

Since each digit is well characterised by the autoencoder of its own kind, we expect the norm of the residual vector computed from the reconstruction using autoencoder of the same kind is less than the residual vector computed from the reconstruction using autoencoder of the other classes.

More specifically, for a given unknown digit, if we compute its relative residual in all 10 reconstructions, classify the unknown digit to the class with the least reconstruction error.

Implementation

Now let us implement the least square residual classifier to classify MNIST digits:

from keras.datasets import mnist
import numpy as np
(x_train, y_train), (x_test, y_test) = mnist.load_data()

We now normalize all values between 0 and 1 and we now flatten the \(28~\times~28\) images into vectors of size 784.

x_train = x_train.astype('float32') / 255.
x_test = x_test.astype('float32') / 255.
x_train = x_train.reshape((len(x_train), np.prod(x_train.shape[1:])))
x_test = x_test.reshape((len(x_test), np.prod(x_test.shape[1:])))

we now partition the x_train based on the ten classes and store in a list.

x_train_list = []
for k in xrange(10):
    components = np.where(y_train == k)[0]
    x_train_list.append(x_train[components])

we now build autoencoder for each digit classes.

from keras.layers import Input, Dense
from keras.models import Model
autoencoder_list = []
for i in xrange(10):
    input_img = Input(shape=(784,))
    encoded = Dense(128, activation='relu')(input_img)
    encoded = Dense(64, activation='relu')(encoded)
    encoded = Dense(32, activation='relu')(encoded)

    decoded = Dense(64, activation='relu')(encoded)
    decoded = Dense(128, activation='relu')(decoded)
    decoded = Dense(784, activation='sigmoid')(decoded)

    autoencoder = Model(input_img, decoded)

    autoencoder_list.append(autoencoder)

First, we'll configure our model to use a per-pixel binary crossentropy loss, and the Adadelta optimizer:

for k in xrange(10):
    autoencoder_list[k].compile(optimizer='adadelta', loss='binary_crossentropy')

Now let's train our autoencoder for 100 epochs:

for k in xrange(10):
    print '--------------------modelling digit class---------------------- ', k
    autoencoder_list[k].fit(x_train_list[k], x_train_list[k],
                    nb_epoch=100,
                    batch_size=256,
                    shuffle=True,
                    )

we now reconstruct the training digits using autoencoders of all 10 classes and compute the respective reconstruction error.

n_train = x_train.shape[0]
y_train_predict = y_train.copy()
for i in xrange(0, n_train, 15):
    x = x_train[i:i+1]
    residual_list = np.ones((10))
    for k in xrange(10):
        x_predict = autoencoder_list[k].predict(x)
        residual = np.linalg.norm(x - x_predict)
        residual_list[k] = residual

    y_train_predict[i] = np.argmin(residual_list)

we now reconstruct the test digits using autoencoders of all 10 classes and compute the respective reconstruction error.

n_test = x_test.shape[0]
y_test_predict = y_test.copy()
for i in xrange(0, n_test, 15):
    x = x_test[i:i+1]
    residual_list = np.ones((10))
    for k in xrange(10):
        x_predict = autoencoder_list[k].predict(x)
        residual = np.linalg.norm(x - x_predict)
        residual_list[k] = residual

    y_test_predict[i] = np.argmin(residual_list)

The autoencoder based least square residual classifier obtains training error of ~0.05 and test error of ~0.05.

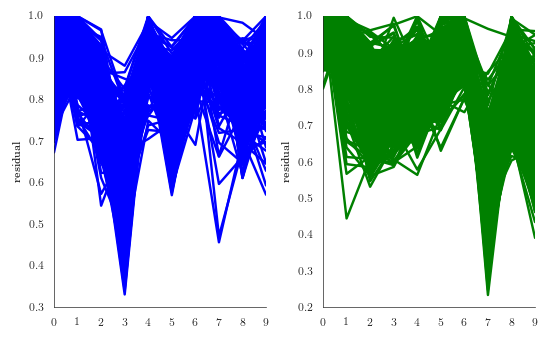
We now show the relative residual norm for all test digit 3 and all test digit 7 in terms of all 10 autoencoders.

We notice in the two figures, that most of the test digits 3 and 7 are best approximated in terms of their own autoencoder.

We show in the figure below the approximation of digit 4 (top) and digit 5 (bottom) obtained from the reconstruction using autoencoders of classes 0 to 9. We notice in the figure, both 4 and 5 are best reconstructed by their own autoencoder.

We show in the figure below the approximation of digit 3 (top) and digit 7 (bottom) obtained from the reconstruction using autoencoders of classes 0 to 9. We notice in the figure, both 3 and 7 are best reconstructed by their own autoencoder.

The layout of this blog is inspired by

Building Autoencoders in Keras

References